Java算法

Java算法学习记录

前言
本文仅用于个人对于数据结构的理解与学习，可能存在诸多不足之处，并且顺序为主播个人的随意的学习顺序，会有诸多杂乱之处。

目录

• KMP算法
  • 暴力匹配
  • KMP
    • 部分匹配表
• 普利姆算法

---

KMP算法

---

应用场景-字符串匹配问题

Str1 = “BBC ABCDAB ABCDABCDABDE”
Str2 = “ABCDABD”

暴力匹配

对于暴力匹配，思路采用的是str1指针逐个右移，直至匹配成功

public class violenceMatch{
   public int violenceMatch(String str1,String str2){
      //将String转化为字符数组
      char [] s1 = str1.toCharArray();
      char [] s2 = str2.toCharArray();
      
      int s1Len = s1.length;
      int s2Len = s2.length;

      int i=0,j=0;
      while(i<s1Len && j<s2Len){
         //如果相等，则让两个指针右移
         if(s1[i]==s2[j]){
            i++;
            j++;
         }
         //否则i指针回溯并且右移一位，j重置为0
         else{
            i=i-j+1;
            j=0
         }
      
      //如果找到，则返回当前索引
      if(j==s2Len){
         return i-j;
      }
   }return -1;
}

public void test1(){
   String str1 = abcdabc;
   String str2 = cda;
   System.out.println(violenceMatch(str1,str2));
}

public void test2(){
   String str1 = asdfghjkl;
   String str2 = azx;
   System.out.println(violenceMatch(str1,str2));
   }
}

KMP

• 假设现在文本串S匹配到 i 位置，模式串P匹配到 j 位置
  • 如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++，继续匹配下一个字符；
  • 如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]。此举意味着失配时，模式串P相对于文本串S向右移动了j - next [j] 位。
    • 换言之，当匹配失败时，模式串向右移动的位数为：失配字符所在位置 - 失配字符对应的next 值，即移动的实际位数为：j - next[j]，且此值大于等于1。

next 数组各值的含义：代表当前字符之前的字符串中，有多大长度的相同前缀后缀。例如如果next [j] = k，代表j 之前的字符串中有最大长度为k 的相同前缀后缀。

此也意味着在某个字符失配时，该字符对应的next 值会告诉你下一步匹配中，模式串应该跳到哪个位置（跳到next [j] 的位置）。如果next [j] 等于0或-1，则跳到模式串的开头字符，若next [j] = k 且 k > 0，代表下次匹配跳到j 之前的某个字符，而不是跳到开头，且具体跳过了k 个字符。

KMP算法包括两个内容：

1. 得到子串的部分匹配表
2. 使用部分匹配表完成 KMP 匹配

1. 部分匹配表

网络上普遍的求解部分匹配表的原理为根据当前位置的字符串求字串的最大相同字符串长度
例如：

字符串 ababc

字符串	前缀	后缀	共有元素	共有元素长度
a	-	-	-	-
ab	a	b	-	-
aba	a、ab	a、ba	a	1
abab	a、ab、aba	b、ab、bab	ab	2
ababc	a、ab、aba、abab	c、bc、abc、babc	-	-

部分匹配表如下：

字符串	a	b	a	b	c
索引	0	1	2	3	4
PMT	0	0	1	2	0

在学校ppt的课件上的next数组求法则以当前位置的之前的字符串求最大相同字符串长度：

T[j]	a	b	a	b	c
j	0	1	2	3	4
next[j]	0	0	0	0	1

next[0] == 0;其余从首位开始；

next数组获取算法代码：

public int [] buildKmpNext(String dest){
   int [] next = new int[dest.length()];
   next[0]=0;
   for(int i =1,j=0;i<dest.length();i++){
      // 当  dest.charAt(i) != dest.charAt(j) 时
      // 需要从 next[j-1] 中获取新的 j
      // 这步骤是 部分匹配表的 核心点
      while(j>0&&dest.charAt(i)!=dest.charAt(j)){
         j=next[j-1];
      }
   }if(dest.charAt(i)==dest.charAt(j)){
      j++;
   }next[i]=j;
}return next;

下为deepseek生成的完整代码

public class KMPExample {
    /**
     * KMP算法实现
     */
    public static int kmpSearch(String text, String pattern) {
        int[] next = getNext(pattern);
        int i = 0;  // 文本串指针
        int j = 0;  // 模式串指针
        
        while (i < text.length() && j < pattern.length()) {
            if (j == -1 || text.charAt(i) == pattern.charAt(j)) {
                i++;
                j++;
            } else {
                j = next[j];  // 关键：利用next数组回退
            }
        }
        
        if (j == pattern.length()) {
            return i - j;  // 匹配成功，返回起始位置
        }
        return -1;  // 匹配失败
    }
    
    /**
     * 获取next数组（主方法）
     */
    public static int[] getNext(String pattern) {
        int[] next = new int[pattern.length()];
        next[0] = -1;
        int i = 0, j = -1;
        
        while (i < pattern.length() - 1) {
            if (j == -1 || pattern.charAt(i) == pattern.charAt(j)) {
                i++;
                j++;
                next[i] = j;
            } else {
                j = next[j];
            }
        }
        return next;
    }
    
    /**
     * 可视化打印next数组
     */
    public static void printNextArray(String pattern) {
        int[] next = getNext(pattern);
        
        System.out.println("模式串: " + pattern);
        System.out.print("索引:   ");
        for (int i = 0; i < pattern.length(); i++) {
            System.out.print(i + "\t");
        }
        System.out.println();
        
        System.out.print("字符:   ");
        for (int i = 0; i < pattern.length(); i++) {
            System.out.print(pattern.charAt(i) + "\t");
        }
        System.out.println();
        
        System.out.print("next:   ");
        for (int val : next) {
            System.out.print(val + "\t");
        }
        System.out.println("\n");
    }
    
    public static void main(String[] args) {
        // 测试各种模式串的next数组
        String[] testPatterns = {
            "ababc",
            "abcdabca",
            "aaaaaa",
            "abcabcd",
            "abababca"
        };
        
        for (String pattern : testPatterns) {
            printNextArray(pattern);
        }
        
        // KMP搜索示例
        String text = "ABABDABACDABABCABAB";
        String pattern = "ABABCABAB";
        int index = kmpSearch(text, pattern);
        
        System.out.println("文本: " + text);
        System.out.println("模式: " + pattern);
        if (index != -1) {
            System.out.println("匹配位置: " + index);
        } else {
            System.out.println("未找到匹配");
        }
    }
}

---

普利姆算法

应用场景-修路问题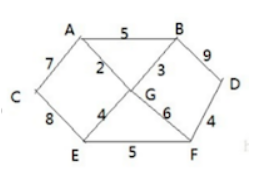

胜利乡有 7 个村庄(A, B, C, D, E, F, G) ，现在需要修路把 7 个村庄连通，各个 村庄的距离用边线表示(权) ，比如 A – B 距离 5 公里

问：如何修路保证各个村庄都能连通，并且总的修建公路 总里程最短?

思路:

• 只满足连通：将 10 条边，连接即可，但是总的里程数不是最小.

• 满足连通，又保证总里程最短：就是尽可能的选择少的路线，并且每条路线最小，保证总里程数最少

最小生成树

修路问题本质就是最小生成树问题，最小生成树(Minimum Cost Spanning Tree)，简称MST。

给定一个 带权的无向连通图，如何选取一棵生成树，使树上所有边上权的总和为最小，这叫最小生成树 ，它有如下特点：

• N 个顶点，一定有 N-1 条边。
• 包含全部顶点。
• N-1条边都在图中。

比如下图：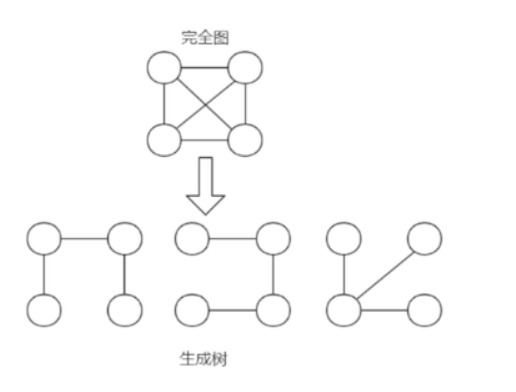

普利姆算法介绍

---

普利姆（Prim）算法求最小生成树，也就是：在包含 n 个顶点的连通图中，找出只有(n-1)条边包含所有 n 个顶点的连通子图，也就是所谓的 极小连通子图
它的算法如下：

1. 设

   • G=(V,E) 是连通网

   • T=(U,D) 是最小生成树

   • V、U 是顶点集合

   • E、D 是边的集合

若从顶点 u 开始构造最小生成树，则从集合 V 中取出顶点 u 放入集合 U 中，标记顶点 v 的visited[u]=1

若集合 U 中顶点 ui 与集合 V-U 中的顶点 vj 之间存在边，则寻找这些边中权值最小的边，但不能构成回路，将顶点 vj 加入集合U中，将边（ui,vj）加入集合 D 中，标记 visited[vj]=1

重复步骤 ②，直到 U 与 V 相等，即所有顶点都被标记为访问过，此时 D 中有 n-1 条边

普利姆算法图解

---

以此为例

1. 从A点开始处理

   与A直连的点有：

   • A,C [7]
   • A,B [5]
   • A,G [2]

   在直连的所有的边中，A,G[2]的权值最小，那么结果是A,G

2. 从A,G开始，找到他们的直连边，但是不包含已经访选择过得边。

   1. A,C[7]
   2. A,B[5]
   3. G,B[3]
   4. G,E[4]
   5. G,F[6]

在以上边中，权值最小的是G,B[3],那么结果是A,G,B

3. 以 A、G、B 开始，找到他们的直连边，但是不包含已经访选择过的边。

   1. A,C [7]
   2. A,B [5]
   3. G,E [4]
   4. G,F [6]
   5. B,D [9]

在以上边中，权值最小的是：G,E [4]，那么结果是：A、G、B、E

4. A、G、B、E → 权值最小的边是 E，F [5] → A、G、B、E、F

5. A、G、B、E、F → 权值最小的边是 F，D [4] → A、G、B、E、F、D

6. A、G、B、E、F、D → 权值最小的边是 A，C [7] → A、G、B、E、F、D、C

那么最终结果为下图：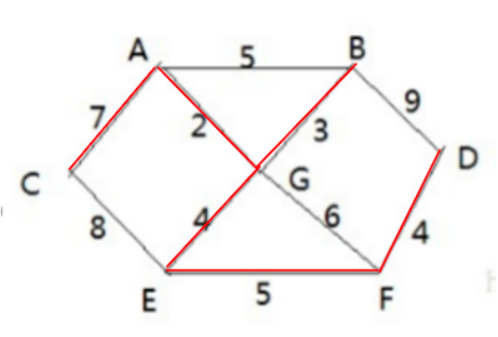

总里程数量为：2+3+4+5+4+7=25